区块链-加密技术-单向散列函数

单向散列函数

哈希函数

什么是哈希？

哈希函数: 将任意数据(二进制字符串) 映射 为固定长度"数字指纹"的单向散列函数，可用于验证数据完整性和保护敏感信息。
使用过程: 输入(任意长度数据) =>【黑盒函数(H: ${0,1}^{*} => {0,1}^{n}$)】 => 固定长度摘要(不可逆推)

核心机制

1. 单向性: 只有加密过程，无解密过程，无法反向计算。
   • 例如，即使得到指纹图片也无法通过指纹映照出个人的基本信息。
2. 确定性: 相同输入即会得到相同输出，根据这点可进行重复验证。
3. 高效性: 能够快速计算大文件或者长文本的哈希值。
4. 固定长度输出: 不管文件与文本的大小，输出的固定字符长度都是相同的。
5. 雪崩效应: 当输入发生轻微变化的时候，输出也会跟着变化。(1位改变 => 50% 变化)

安全机制

1. 抗原像攻击(PreImage Resistance): 已知 hash = "a3b5c7d8....." ，需找到任意 input 使得 H(input) = hash。
   • 该攻击场景: 找到一个明文使其加密为已知 hash值，需通过暴力尝试 $2^n$ 个可能性输入。例如，在SHA-256的情况下，n=256。理论上可能，实际上无法实现。
2. 第二原像攻击(Second PreImage Resistance): 已知 xx.pdf 经计算后的 hash = "x1y2z3..."，需伪造 evil-xx.pdf 使得 H(evil-xx.pdf) = "x1y2z3..."
   • 该攻击场景: 已知明文与哈希值，找到另一个明文使其加密后哈希值相同，需经过 $2^n$ 次碰撞尝试。
3. 抗碰撞攻击(Collision Resistance): 找出任意两个不同的x,x'，使得h(x)=h(x')是困难的。
   • 生日攻击(Birthday Attack): 在较少的尝试次数下,两组数据产生相同哈希值的概率可能比直觉预期要高。
     • 简单来说，假设寻找第二原像攻击需要$2^n$次尝试而寻找任意碰撞据生日攻击的原理，只需要 $2^{\frac{n}{2}}$ 次尝试即可成功。
     • 实际安全强度 = min(原像强度, 碰撞强度)
       = min(n, $\frac{n}{2}$)
       = $\frac{n}{2}$
     • 依据 木桶原理：安全性取决于最弱环节。
   • 为了抵御生日攻击，现代哈希函数的输出长度通常至少为 256 比特（如 SHA-256），这样需要 $2^{128}$ 次尝试，这远超目前计算机的算力极限。即便使用量子计算机也需要$2^{\frac{256}{3}}$次尝试。

为什么需要哈希？

核心问题:在不可信的环境中，如何高效验证大量数据的完整性和真实性？

应用场景	解决的问题	价值体现	使用算法
文件传输校验	网络传输中的数据损坏/篡改	用64个字符验证10GB等大文件	SHA-256
密码存储	数据库泄漏导致密码暴露	不存储明文，无法反推	bcrypt/Argon2
数字签名	文件来源和完整性证明	防止伪造和抵赖	SHA-256
区块链	分布式账本防篡改	任何修改导致链断裂	SHA-256
版本控制	代码变更追踪	每次提交唯一标识	SHA -> SHA-256
数字去重	云存储空间浪费	快速识别重复文件	MD5/SHA-256

哈希算法的价值 = 效率提升 × 安全保障

区块链中的哈希应用

区块

什么是区块

简化的 区块头结构 如下:

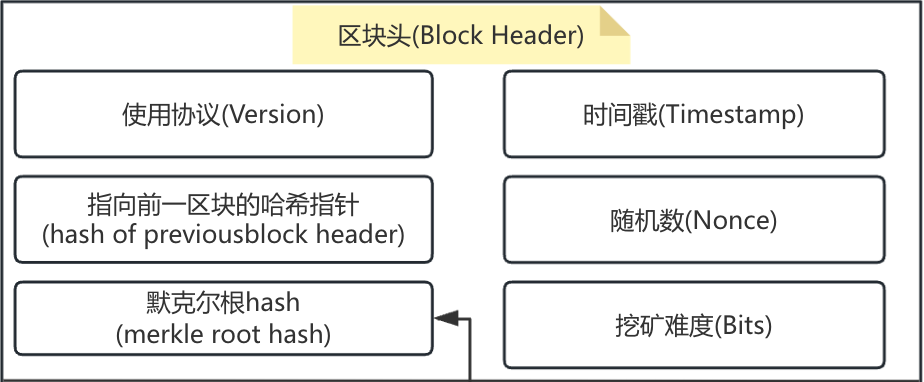
其中，Merkle root hash 保存 Block Body 中的内容不被篡改，所以只需要计算Block Header 就可保证区块内容不被篡改，计算哈希只针对于Block Header。

简化的 完整的区块 如下：

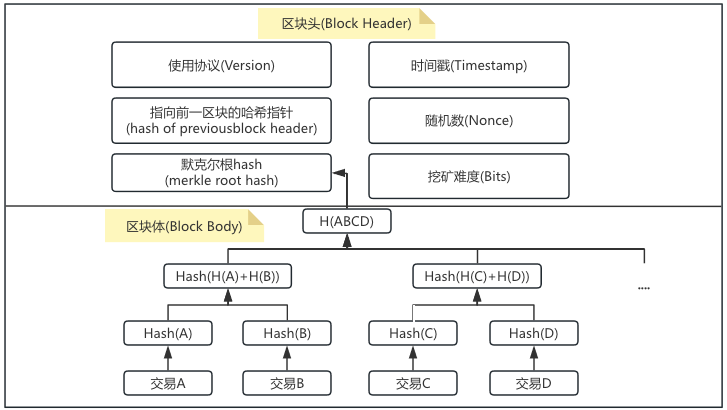
• 区块哈希 = SHA256(所有上述内容)
  • 区块链中每个区块生成的唯一标识符，类似于区块的身份证，唯一的不变的。
  • 它通过对区块内容（包括交易数据、前一个区块的哈希值和时间戳）应用哈希函数运算生成，这串唯一的字符串确保了数据的完整性。
  • 如果区块中的任何细节被更改。由于雪崩效应，哈希值就会完全改变。有助于维护系统的安全性和信任。

区块如何链接

区块链: 一个个区块组成的链条，每个区块通过 previous_hash 知道它的前一个区块，但不知道后续的，这是单向链表的结构。

创世区块(genesis block)：人工创建，不是挖矿产生的，没有前一个区块，previous_hash = "0" 或 全为0。

• 传统链表用内存地址作为指针，区块链以哈希值作为指针。优势在于：
  • 无法伪造 2. 自动验证 3. 跨网络传输。

为什么无法篡改

由于，每个区块记录前一个区块的哈希，形成链条；修改任何历史区块都会导致链条断裂，根据哈希的雪崩效应，会被立即被发现。

工作量证明PoW（核心机制）

• 挖矿本质：寻找Nonce
• 难度目标
• 比特币挖矿演示
• 代码示例：PoW实现

Merkle树（高效验证）

• Merkle树结构
• 如何验证交易
• SPV轻节点
• 代码示例：Merkle树构建

地址生成（实用）

• 比特币地址：Hash160
• 以太坊地址：Keccak256
• 代码示例：生成地址

常见哈希算法

MD5 (不安全，了解)

SHA-1 (已被破解)

SHA-256（比特币使用）

Keccak256（以太坊使用）

算法对比与选择

代码实现

Python 实现 SHA-256

实现简单区块链

实现 Merkle 树

附录

参考文章

哈希函数-生日悖论