区块链-区块结构解析

区块

什么是区块

简化的 区块头结构 如下:

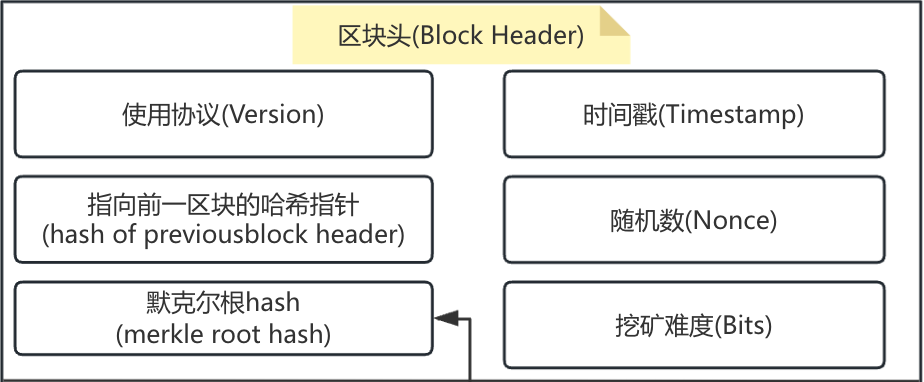
其中，Merkle root hash 保存 Block Body 中的内容不被篡改，所以只需要计算Block Header 就可保证区块内容不被篡改，计算哈希只针对于Block Header。

简化的 完整的区块 如下：

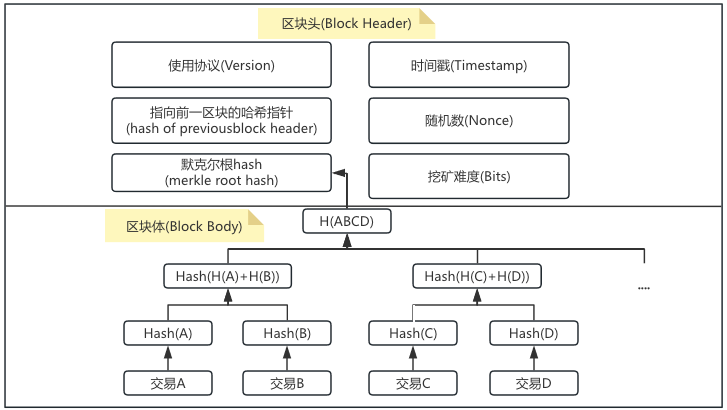
• 区块哈希 = SHA256(所有上述内容)
  • 区块链中每个区块生成的唯一标识符，类似于区块的身份证，唯一的不变的。
  • 它通过对区块内容（包括交易数据、前一个区块的哈希值和时间戳）应用哈希函数运算生成，这串唯一的字符串确保了数据的完整性。
  • 如果区块中的任何细节被更改。由于雪崩效应，哈希值就会完全改变。有助于维护系统的安全性和信任。

区块如何链接

区块链: 一个个区块组成的链条，每个区块通过 previous_hash 知道它的前一个区块，但不知道后续的，这是单向链表的结构。

创世区块(genesis block)：人工创建，不是挖矿产生的，没有前一个区块，previous_hash = "0" 或 全为0。

以下以blockchain.com作为示例：

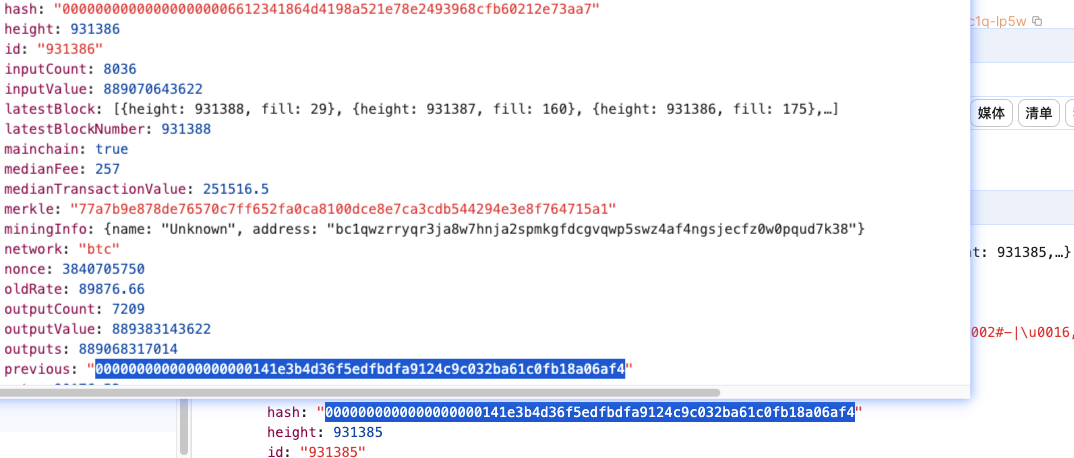
• 传统链表用内存地址作为指针，区块链以哈希值作为指针。优势在于：
  • 无法伪造 2. 自动验证 3. 跨网络传输。

为什么无法篡改

由于，每个区块记录前一个区块的哈希，形成链条；修改任何历史区块都会导致链条断裂，根据哈希的雪崩效应，会被立即被发现。

挖矿与工作量证明

挖矿本质

挖矿: 计算数学问题，寻找一个特殊的Nonce，使得区块哈希满足难度要求。

Nonce: 作为一个随机数参与运算，其范围为0-32位的整数(0-4294967295)，区块头中唯一可以随意修改的字段，每次挖矿可尝试改变一次。

由于给定区块完整的区块内容，需要找到一个哈希值 < 目标值，因为哈希函数是单向的，无法反推，唯一的方式只能通过暴力尝试。通过不断的改变Nonce计算哈希直到找到符合条件的。

工作量证明

工作量证明(POW): 通过大量的尝试得到符合要求的结果，这个过程就是工作量证明。（difficult to solve ,but easy to find ）

在上面提到 计算出的哈希值 需要小于 目标值，这个目标是一个256位的数值，区块哈希必须要小于这个值才能有效。

难度的表示方式

表示1：Bits（紧凑格式）

存储在区块头中：32位

格式：0xAABBCCDD
      ↑↑ ↑↑↑↑↑↑
     指数 尾数

例如：0x1d00ffff

表示2：Difficulty（难度值）

相对于最低难度的倍数

最低难度 = 1.0（创世区块）
当前难度 = 60,000,000,000,000+（60万亿+）

难度越高 = 挖矿越难

Bits 转 Target 的公式：Bits格式：0xAABBCCDD 指数 = AA 尾数 = BBCCDD Target = 尾数 × 256^(指数 - 3)

挖矿过程

Merkle树

Merkle树结构

Merkle Tree 是什么

• 叶子节点 = hash(tx)
• 非叶子节点 = hash(left || right)
• 根节点 = Merkle Root

为什么不用一个 hash 就行

• 大量交易如何高效校验
• 防篡改 vs 局部验证

Merkle Tree 的特性

• 防篡改性
• 对数级验证复杂度 O(log n)
• 任意叶子变化 → 根变化

常见变体（了解即可）

• Binary Merkle Tree
• Merkle Patricia Trie（以太坊用）

如何验证交易(Merkle Proof)

什么是 Merkle Proof

• 又叫 Merkle Path / Authentication Path
• 包含：
  • 交易 hash
  • 一路上的兄弟节点 hash

验证一笔交易是否在区块中

• 已知：
  • tx hash
  • Merkle proof
  • block header 中的 Merkle root
• 本地计算是否能还原 root

复杂度分析

• 空间：log2(n) 个 hash
• 时间：log2(n) 次 hash

实际例子（非常重要）

• 用 4 / 8 笔交易手算一棵树

SPV轻节点

1. 什么是 SPV（Simplified Payment Verification）
   • 不下载完整区块
   • 只保存 block header（80 bytes）
2. SPV 轻节点如何验证交易
   • 下载区块头链
   • 获取 Merkle Proof
   • 验证 Merkle Root
3. SPV 的信任假设
   • 信任最长链
   • 不验证所有交易合法性
4. SPV 的安全边界
   • 不能防止：
     • 双花的复杂攻击
     • 恶意矿工协同
   • 为什么轻节点 ≠ 全节点